CORRECCIÓN DE ERRORES

El cuadernillo de recuperación del 1er trimestre de 2º de la ESO, se ha actualizado. Podeis descargarlo en este enlace:

CUADERNILLO DE RECUPERACIÓN DEL 1er TRIMESTRE DE 2º ESO

ACTIVIDADES PARA LA RECUPERACIÓN DE LA ASIGNATURA EPVA EN SEPTIEMBRE.

A continuación podéis descargar los cuadernillos por trimestres correspondientes a los cursos de 1º y 2º de la ESO.

Habrá que entregarlos realizados el día 3 de septiembre en el aula F2 para tener derecho a realizar el examen. La nota final se pondera de la siguiente manera: 60% las láminas y 40% el examen. De ahí, la importancia de entregar las láminas ya que el no hacerlo supone suspenso automático.

¡Atención! Debereis consultar en el informe de EPVA, si alguno de los trimestres estan aprobados. De tal modo no es necesario realizar las tareas del cuadernillo de los trimestres aprobados y la parte correspondiente del examen.

CUADERNILLOS POR TRIMESTRES DE RECUPERACIÓN DE 1º ESO*

1. Descargar cuadernillo del 1er trimestre.
2. Descargar cuadernillo del 2º trimestre.
3. Descargar cuadernillo del 3er trimestre.

CUADERNILLOS POR TRIMESTRES DE RECUPERACIÓN DE 2º ESO*

1. Descargar cuadernillo del 1er trimestre
2. Descargar cuadernillo del 2º trimestre
3. Descargar cuadernillo del 3er trimestre

*algunos archivos pesan mas de 20 megas, así que puede tardar algunos minutos en descargar.

FECHA DE ENTREGA Y REALIZACIÓN DEL EXAMEN: 3 de septiembre a las 13 horas en el aula F2.

Para cualquier duda podeís mandar un email a: antoniogalaplastica@gmail.com

Ilusiones ópticas

ILUSIONES ÓPTICAS

Si toda la información que tenemos nos llega a través de los sentidos. 
¿Qué pasa si nuestros sentidos nos engañan?

A veces, nuestros sentidos captan la realidad, pero se produce un error cuando interpretamos
las características sensoriales de lo que percibimos (por ejemplo, en la estimación del tamaño 
o color de un objeto, o en la captación de la figura y el fondo).

Las ilusiones ópticas son el resultado de la interpretación o suposición que hace el cerebro de las
imágenes percibidas por los ojos. La publicidad, a veces recurre a este tipo de ilusiones ópticas para 
captar nuestra atención. En este vídeo publicitario de una marca de coches tenemos una variada 
muestra de ellas.

  


Existen en internet existen interesantes aplicaciones sobre las ilusiones ópticas 
como las que tienes a continuación:

Para saber mas:

• Web interactiva para ver y analizar las diferentes ilusiones ópticas
• Catálogo sobre ilusiones ópticas.
• Enciclopedia interactica de la Percepción Visual.
• Anamorfosis.
• Escher

ACTIVIDAD. Cómo hacer ilusiones ópticas: 

1a PROPUESTA

2a PROPUESTA:

•  Increible página, ( anmorfosis en folios) 

•  Imágenes ( pinterest).

PERSPECTIVA CÓNICA

El Sistema Cónico, también llamado Perspectiva Cónica, utiliza el sistema de Proyección Cónica sobre un plano de proyección llamado Plano del Cuadro (PC).
La imagen que obtenemos es la representación de un objeto o espacio tal y como lo ve el observador, por lo que es una representación esencialmente subjetiva.

En la siguiente imagen podéis ver los distintos elementos que intervienen en este tipo de perspectiva que es, dentro de los Sistemas de Representación aquél que más se acerca a la visión humana (monocular).

Haced clic sobre ella para ampliarla y verla con más detalle.

En la imagen os enlazo una construcción interactiva de GeoGebra para que entendáis mejor cómo afecta el punto de vista, la altura de la Línea de Horizonte, así como las dimensiones de la habitación en la visión que tenemos de ésta.

Si hacéis clic nuevamente sobre la imagen podréis acceder a otra construcción interactiva.

Es interesante que modifiquéis las dimensiones de los planos y tratéis de situarlos según una serie de premisas.

Por ejemplo:

Sitúa un poster de 1 m de altura y 1/2 de anchura sobre la pared de la izquierda de forma que quede situado a 1 m de profundidad y a una altura de metro y medio...

Coloca en el suelo una alfombra de 2 m por 3m ...,etc.

Os será de todas formas mucho más fácil hacerlo sobre la construcción que tenéis debajo.

Igualmente en esta otra imagen tenéis el enlace al applet de GeoGebra, donde podeis cambiar los parámetros que influyen en la construcción y percepción de la perspectiva cónica.

 Si pulsáis sobre la imagen accederéis a otra construcción en la que podréis situar el punto de fuga así como las líneas que se dirigen hacia él sobre distintos cuadros del pintor hiperrealista Antonio López.















Vamos a ver cómo se puede hacer un dibujo realista con la perspectiva cónica.

SIMETRIAS

SIMETRIAS

La simetría es una de las características que podemos observar en las composiciones visuales y plásticas. Básicamente es una relación entre las figuras, según su ubicación en la imagen.

En nuestros cursos trabajaremos básicamente la simetría axial y la simetría central.

Un posible CONCEPTO GENERAL general de simetría en una imagen:
Es la composición visual donde cada punto equidista (igual distancia) respecto al elemento visual de simetría.

SIMETRÍA AXIAL:

Es la composición visual donde cada punto equidista (igual distancia) de un EJE.

En este caso, en todas las imágenes de simetría axial tendríamos que poder identificar un eje, o sea un linea recta, que tuviera a sus lados, la misma imagen pero invertida, de tal manera que cada punto estuviera a igual distancia de su simétrico al otro lado del eje.

Ejemplos de simetría axial:

  

 

 

 

SIMETRÍA CENTRAL:

Es la composición visual donde cada punto equidista (igual distancia) de un PUNTO.

En este caso, en todas las imágenes de simetría central tendríamos que poder identificar un punto o centro, que tuviera a sus alrededor la misma imagen pero invertida, de tal manera que cada punto estuviera a igual distancia de su simétrico al otro lado del punto o centro.

EJEMPLOS DE SIMETRÍA CENTRAL:

Algunos ejemplos son más geométricos, otros aproximados, hay ejemplos del diseño, la naturaleza, entre otros.

    

  

APLICACIONES PARA HACER EJERCICIOS DE SIMETRÍAS:

Práctica de simetría axial

Práctica de simetría radial

Realizar imágenes de dichas simetrías y enviar a: antoniogalaplastica@gmail.com 

MOSAICOS….transformaciones artisticas

Arte y Mosaicos

Muchos conocen en Matemática a un artista del teselado, que asombra con sus creaciones

Cornelius Escher 

M.C. Escher se inspiró en los impresionantes alicatados geométricos de la Alhambra, para crear sus famosos mosaicos y tranformaciones con figuras de animales y otros seres.

. En el primer viaje que realizó Escher a la Alhambra, en 1922, dibujó las cintas que configuraban uno de los alicatados de la Sala Mexuar de uno de los palacios Nazaríes de la Alhambra.

Inspirados en sus obras podemos crear las nuestras, con un poco de GEOMETRIA y mucha imaginación, en muchos casos haciendo uso de las tecnicas de mozaicos como el hueso, o la pajarita

Obs: En todos los caso donde se use la isometria, se relizarà con papel de calcar o recortando sucesivamente y copiando.

TRANSLACION

1- Tomar una figura que cubra el plano y cuyos lados sean paralelos.

2- En uno de los lados realizar un dibujo de vèrtice a vertice

3- Compiar el dibujo hecho y transladarlo al lado opuesto

4-Repetir el proceso con los otros lados

5- Usar de patron y copiarlo sobre una hoja cubriendo la superficie

o recortandolo en hojas y pegandolo luego para cubrir la superficie

Metodo individual

En todos los lados

En distintas figuras que cumplan con la propiedad

Por rotación inspirado en el hueso

El procedimiento es igual a la de la construcciòn del hueso (mosaico nazari)

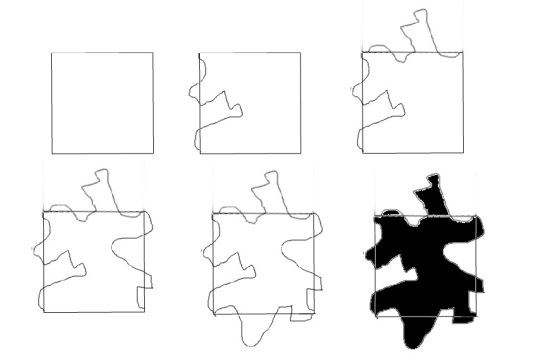
1- Construye un cuadrado
2- Dibuja en uno de los lados del cuadrado

3- Copialo, y rotalo 90º de tal modo que el vèrtice sea punto de rotaciòn copia o pega

4- Toma el otro lado y realiza el dibujo deseado. Copialo en papel de calcar o recortandolo y transladando a otra hoja.

5- Con rotaciòn de 90º con el vèrtice como centro de rotaciòn termina la figura.

6- Observa lo que construiste, usa tu imaginaciòn y luego copialo en una hoja o recorta en distintos colores y pegalos sin superponer y cubriendo toda la superficie

º
En mi caso te dejo un ejemplo que me parecieron brujas.

Mosaico inspirado en la pajarita

El procedimiento llega al mismo dibujo que la pajarita pero más libre

1- Se realiza en una figura regular

2-En uno de los lados hacer un dibujo (copiarlo)

3- En el lado consecutivo realiza una rotaciòn de 60º con el vèrtice como centro de rotaciòn

4- En el otro lado, divide a la mitad, en una mitad realiza un dibujo y luego tomando el punto medio como centro de rotaciòn realiza un giro de 180º.

Ejemplo1

MOSAICO DE FLORES

Haciendo uso de la pajarita

En este caso tomando la pajarita y las medianas del triangulo, pueden formarse tres rosas, todo acorde al gusto del artista

Practica diferentes tipos de teselaciones con la siguiente aplicación: